Exercício 6

Idem ao 5 mas para adjacente

Exercício 5

Construir numa Matriz de incidência e passar a matriz de incidência para adjacencia

Exercício 4

Imprime uma Lista em Forma de Matriz.
Ele percorre cada índice do vetor da lista e faz um for para percorre os nodes se existir um vértice igual ao índice do for será impresso o peso da aresta se não imprime zero.

Exercício 3

É para mostrar a quantidade de memória utilizada
Na matriz quadrada temos que multiplicar o nº de vértice+1 (já q não estou utilizando o índice zero) ao quadrado, somo ao vetor de pesos que é nº de vértice+1 e +1 que é o qtdnos e por fim multiplico tudo por 4 que são os 4 bytes utilizados por cada int
Na Lista é um pouco mais complicada 1º temos que saber que um vértice usa 3 ints temos dois vetores um na lista e o outro para os pesos e também temos que saber a quantidade de nodes, representado pelo "y" que é incrementado a cada vértice diferente de zero agora fazemos (((quantidade de vertices +1)*2)+(y*3))*4bytes

mais métodos

o get aresta retorna o peso da aresta se ela não existir será retornado zero
o size retorna apenas a quantidade de vértices
o showLista exibe a lista na tela

PushLista

Como já dito esse método insere o vértice na lista e também serve para atualizar o peso do arco

Método PushNode

ele apenas cria um nó que depois será lançado na lista através do PushLista

Dimencionar

Assim como na matriz o método dimensionar gera o grafo no caso uma Lista com os ponteiros indicando NULL

Classe Lista

finalmente a classe lista os métodos serão detalhados a seguir

Classe Node

Como em lista encadeada também vamos precisar da classe Node, a única diferença é que invés de valor temos vértice e peso e seu métodos de get e set

Lista de Adjacencia

A lista substitui a matriz em casos que os vértices se encontram muito esparsos tendo como objetivo um menor consumo de memória.
Ela é composta de um vetor onde o índice representa os vértices e que são ponteiros para uma lista encadeada contendo o peso da aresta e o vértice, em separado temos outro vetor para o peso dos nós.

métodos

//ele cria a matriz e preenche ele com zeros isso se o tamanho for maior que zero
void Grafo::dimensionar(int tamanho) {
if (tamanho > 0) {
qtdnos = tamanho;
pesos = new int[qtdnos];
matriz = new int*[qtdnos];
for(int i = 0; i < qtdnos; i++){matriz[i] = new int[qtdnos];}
for(int k = 0; k < qtdnos; k++){
for(int l = 0; l < qtdnos; l++){matriz[k][l]=0;}
}
}
else {qtdnos = 0;pesos = NULL;matriz = NULL;
}
}

void Grafo::setAresta(int i, int j){matriz[i][j] = 1;}
void Grafo::setAresta(int i, int j, int peso){matriz[i][j] = peso;}
int Grafo::getAresta(int i, int j){return matriz[i][j];}
void Grafo::setPeso(int i, int peso){pesos[i] = peso;}
int Grafo::getPeso(int i){return pesos[i];}
int Grafo::size(){return qtdnos;}
//imprime a matriz na tela
void Grafo::showMatriz(){
for(int i = 0; i < qtdnos; i++){
for (int j = 0; j < qtdnos; j++){
cout << matriz[i][j] << " ";
}
cout << endl;
}
}
//imprime os pesos na tela
void Grafo::showPesos(){
for(int i = 0; i < qtdnos; i++)
cout << "peso "<<< " ";
cout << endl;
for(int i = 0; i < qtdnos; i++)
cout << pesos[i] << " ";
cout << endl;
}

Grafo Adjacente

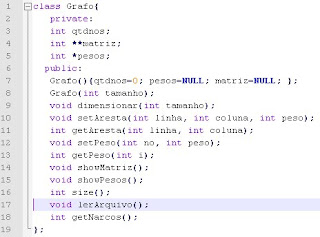Essa classe gera um grafo de matriz adjacente
é composta por: qtdnos (quantidade de nós) usado para dimensionar a matriz, a matriz em si e o peso um vetor para armazenar o peso de cada vértice.
Grafo() é o construtor do grafo inicializando a matriz com NULL, já que **matriz é um ponteiro e evitando assim um pouco de dor de cabeça
os gets e sets tem o mesmo conceito dos códigos anteriores.

GRAFOS

Os grafos são estruturas de dados amplamente utilizadas, mas ao contrário das outras estruturas vistas até agora ele não é uma forma de armazenar dados e sim de solucionar problemas. Pode ser utilizado em varias áreas como num mapa para achar o menor caminho a ser percorrido ou em máquinas para cortar peças de uma prancha (como na fabricação de móveis) com o menor desperdício possível.
O grafo é composto pelo vértice (nó) e a aresta (arco), os vértices são ligados entre si pelas arestas. Um exemplo para entender-mos melhor seria uma cidade (vértice) e uma estrada (aresta), onde a estrada liga a cidade a outras, ele pode ser mão única, ou seja, você pode sair de uma cidade pra outra mas não pode voltar por ela, em grafos isso é chamado de arco "dirigido" é representado com uma seta mostrando a direção, também pode existir uma aresta "não dirigida" sem seta, onde se pode ir e voltar pelo mesmo arco.caso haja apenas uma aresta dirigida o grafo será considerado dirigido.

A 1ª aplicação de grafos foi feita por Euler, provando que só é possível percorrer todos os nós de um grafo sem repetir nenhuma aresta retornando ao vértice de origem, se o grau (nº de arcos ligados a um nó) seja par, esse conceito é denominado caminho euleriano.