Exercício 6

Idem ao 5 mas para adjacente

Exercício 5

Construir numa Matriz de incidência e passar a matriz de incidência para adjacencia

Exercício 4

Imprime uma Lista em Forma de Matriz.
Ele percorre cada índice do vetor da lista e faz um for para percorre os nodes se existir um vértice igual ao índice do for será impresso o peso da aresta se não imprime zero.

Exercício 3

É para mostrar a quantidade de memória utilizada
Na matriz quadrada temos que multiplicar o nº de vértice+1 (já q não estou utilizando o índice zero) ao quadrado, somo ao vetor de pesos que é nº de vértice+1 e +1 que é o qtdnos e por fim multiplico tudo por 4 que são os 4 bytes utilizados por cada int
Na Lista é um pouco mais complicada 1º temos que saber que um vértice usa 3 ints temos dois vetores um na lista e o outro para os pesos e também temos que saber a quantidade de nodes, representado pelo "y" que é incrementado a cada vértice diferente de zero agora fazemos (((quantidade de vertices +1)*2)+(y*3))*4bytes

mais métodos

o get aresta retorna o peso da aresta se ela não existir será retornado zero
o size retorna apenas a quantidade de vértices
o showLista exibe a lista na tela

PushLista

Como já dito esse método insere o vértice na lista e também serve para atualizar o peso do arco

Método PushNode

ele apenas cria um nó que depois será lançado na lista através do PushLista

Dimencionar

Assim como na matriz o método dimensionar gera o grafo no caso uma Lista com os ponteiros indicando NULL

Classe Lista

finalmente a classe lista os métodos serão detalhados a seguir

Classe Node

Como em lista encadeada também vamos precisar da classe Node, a única diferença é que invés de valor temos vértice e peso e seu métodos de get e set

Lista de Adjacencia

A lista substitui a matriz em casos que os vértices se encontram muito esparsos tendo como objetivo um menor consumo de memória.
Ela é composta de um vetor onde o índice representa os vértices e que são ponteiros para uma lista encadeada contendo o peso da aresta e o vértice, em separado temos outro vetor para o peso dos nós.

métodos

//ele cria a matriz e preenche ele com zeros isso se o tamanho for maior que zero
void Grafo::dimensionar(int tamanho) {
if (tamanho > 0) {
qtdnos = tamanho;
pesos = new int[qtdnos];
matriz = new int*[qtdnos];
for(int i = 0; i < qtdnos; i++){matriz[i] = new int[qtdnos];}
for(int k = 0; k < qtdnos; k++){
for(int l = 0; l < qtdnos; l++){matriz[k][l]=0;}
}
}
else {qtdnos = 0;pesos = NULL;matriz = NULL;
}
}

void Grafo::setAresta(int i, int j){matriz[i][j] = 1;}
void Grafo::setAresta(int i, int j, int peso){matriz[i][j] = peso;}
int Grafo::getAresta(int i, int j){return matriz[i][j];}
void Grafo::setPeso(int i, int peso){pesos[i] = peso;}
int Grafo::getPeso(int i){return pesos[i];}
int Grafo::size(){return qtdnos;}
//imprime a matriz na tela
void Grafo::showMatriz(){
for(int i = 0; i < qtdnos; i++){
for (int j = 0; j < qtdnos; j++){
cout << matriz[i][j] << " ";
}
cout << endl;
}
}
//imprime os pesos na tela
void Grafo::showPesos(){
for(int i = 0; i < qtdnos; i++)
cout << "peso "<<< " ";
cout << endl;
for(int i = 0; i < qtdnos; i++)
cout << pesos[i] << " ";
cout << endl;
}

Grafo Adjacente

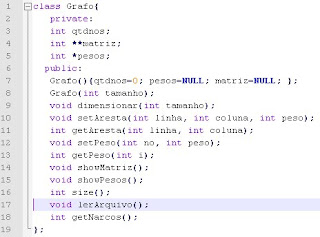Essa classe gera um grafo de matriz adjacente
é composta por: qtdnos (quantidade de nós) usado para dimensionar a matriz, a matriz em si e o peso um vetor para armazenar o peso de cada vértice.
Grafo() é o construtor do grafo inicializando a matriz com NULL, já que **matriz é um ponteiro e evitando assim um pouco de dor de cabeça
os gets e sets tem o mesmo conceito dos códigos anteriores.

GRAFOS

Os grafos são estruturas de dados amplamente utilizadas, mas ao contrário das outras estruturas vistas até agora ele não é uma forma de armazenar dados e sim de solucionar problemas. Pode ser utilizado em varias áreas como num mapa para achar o menor caminho a ser percorrido ou em máquinas para cortar peças de uma prancha (como na fabricação de móveis) com o menor desperdício possível.
O grafo é composto pelo vértice (nó) e a aresta (arco), os vértices são ligados entre si pelas arestas. Um exemplo para entender-mos melhor seria uma cidade (vértice) e uma estrada (aresta), onde a estrada liga a cidade a outras, ele pode ser mão única, ou seja, você pode sair de uma cidade pra outra mas não pode voltar por ela, em grafos isso é chamado de arco "dirigido" é representado com uma seta mostrando a direção, também pode existir uma aresta "não dirigida" sem seta, onde se pode ir e voltar pelo mesmo arco.caso haja apenas uma aresta dirigida o grafo será considerado dirigido.

A 1ª aplicação de grafos foi feita por Euler, provando que só é possível percorrer todos os nós de um grafo sem repetir nenhuma aresta retornando ao vértice de origem, se o grau (nº de arcos ligados a um nó) seja par, esse conceito é denominado caminho euleriano.

Desafio

/*
Para quem não lembra do exercício é pegar os dados apresentados em forma de pós ordem e passar para hierárquica.
Criei um novo main para o desafio, a intenção é lançar os dados numa lista encadeada e repassa-los do final para o inicio da lista montando assim a arvore, ou seja, os valores são 20, 35, 45, 40, 30, 55, 60, 90, 70, 50 e inserindo os dados de trais pra frente é possível recuperar a arvore(imagem a baixo) , depois é só usar os métodos já existentes.

Estou usando os mesmo valores das postagens anteriores para melhor compreensão.
Então mãos a obra
*/

#include
#include
#include "btree.h"
#include "fila.h"
#include

using namespace std;

int main(){

btree a1;
fila fila1;
//Inserindo os dados em pós ordem
fila1.push_final(20);
fila1.push_final(35);
fila1.push_final(45);
fila1.push_final(40);
fila1.push_final(30);
fila1.push_final(55);
fila1.push_final(60);
fila1.push_final(90);
fila1.push_final(70);
fila1.push_final(50);

int x=0;
while (x!= -999){// esse trecho percorre toda a arvore
x=fila1.pop_final();//a variável "x" recebe o ultimo valor da lista
if (x!= -999)//se o x for diferente de -999 (lista vazia)
{
a1.push(x);//o valor de x é inserido na arvore
}// fecha o if
}// fecha o while
cout << "\n\n" <<"Hierarquica I" << endl;
a1.hierarquica1(); //executa o método hierarquica1 para a arvore atual
cout << "\n" <<"Hierarquica II" << endl;
a1.hierarquica2();//e o hierarquica2
// PAUSE NO PRGRAMA
system("PAUSE");
return 0;
}

fila.h

/*
Estou postando esse biblioteca derivada de uma exercício do 2 bimestre sobre lista encadeada, que vai ser usado para revolver o desafio que o Eduardo deixou
*/

#ifndef _LISTA_H
#define _LISTA_H

#include
#include

using namespace std;

class no{ //Classe NÓ
private:
int valor;
no *prox;
public:
no(){valor=0;prox=NULL;}
void setvalor(int v){valor=v;}
void setprox (no *p){prox=p;}
int getvalor(){return valor;}
no *getprox(){return prox;}
};

class fila{ // Classe FILA
private:
no *inicio;
no *final;
public:
fila() {inicio=final=NULL;}
void push_final(int v);
int pop_final();
} ;

void fila::push_final(int v){
no *aux;
aux=new(no);
aux->setprox(NULL);
aux->setvalor(v);
if (final!=NULL)
{
final->setprox(aux);
final=aux;
}
else
inicio=final=aux;
}

int fila::pop_final(){
no *aux1;
no *aux;
if(inicio!=NULL) //verifico se há nós na fila
{
int res=0; //cria variavel para guardar o valor do no e inicializo ela...
aux1=inicio; //posiciono os ponteiros no inicio e no final da fila
aux=final;
if(inicio!=final) //verifico se a pilha possui 2 nós ou mais...
{
while(aux1->getprox()!=final)
/*se a condição acima for verdadeira(ou seja, possui mais de um nó....uso este WHILE para navegar com o AUX1 até o penultimo nó da fila... */
{
aux1=aux1->getprox(); //comando para o AUX1 passar para o nó seguinte....
}
//qd sair do WHILE estarei com o AUX1 no penultimo nó e o AUX no ultimo nó....
res=aux->getvalor(); //pego o valor do ultimo nó e jogo na variavel res...
delete(aux); //libero o espaço de memoria que era ocupado pelo AUX (ultimo nó)
aux1->setprox(NULL); //Configuro o PROX do AUX1 para ser NULL( porque ele passou a ser
//o ultimo nó)....
final=aux1; //Posiciono o final da fila no nó representado por AUX1
return res; //retorna o valor da variavel res
}
else//Caso a fila possua somente um nó...
{
res=aux->getvalor(); //variavel res recebe o valor nó...
delete(aux); //libero o espaço de memoria do nó....
inicio=final=NULL; //como nao tera nós na fila configuro o INICIO e FINAL para NULL
return res; //retorna o valor da variavel res....
}
}
else
/* caso não haja nós na fila o metodo deve retornar -999 ....(tentei retornando NULL mas dá erro)*/
{
return -999 ;
}
}
#endif

DEGENERADA, CHEIA E COMPLETA

/*
Estou postando os trechos dos 3 exercícios q faltavam
a definição é:
degenerada - um nó por nível, completa - as folhas estão no ultimo e penúltimo nível, cheia - as folhas estão apenas no ultimo nível (eu acho)
*/

//btree.h

class btree{

private:

bool Degenerada(ptrno);
int completa(ptrno, int);
int cheia(ptrno, int);

public:

bool Degenerada();
int completa();
int cheia();

};
//chamada do método degenerada
bool btree:: Degenerada(){
Degenerada (raiz);//passando a raiz como parametro
}

bool btree:: Degenerada(ptrno r){
//verifica se a arvore tem mais de 1 nó por nível
if (r->getEsq()!=NULL && r->getDir()!=NULL)
return false;//se sim retorna falsa
else{
//condição para o ultimo nó
if (r->getEsq()==NULL && r->getDir()==NULL)
return true;
//esse trecho faz o zig-zag da arvore
if (r->getEsq()!=NULL)//vá para a esquerda se o nó ñ for NULL
return Degenerada(r->getEsq());
else
return Degenerada(r->getDir());//caso contrário vá para a direita
}
}
/*inicializa o método passando como parâmetro raiz e zero, qp é o nível de cada nó e será utilizado para a comparação dos nós, se o método retornar ao main zero é porque a arvore está vazia ou não é completa*/
int btree:: completa(){
completa (raiz, 0);
}

int btree:: completa (ptrno r, int qd){
/*quando chegar ao ultimo nó ou a arvore estiver vazia retorna qd*/
if (r==NULL){ return qd;}
else{
/* caso contrário qd incrementa 1, assim a arvore tem 1 ou mais nós*/
qd++;
/*declarei as variáveis "e" (esquerda) e "d"(direita)para melhor entendimento*/
int e = completa(r->getEsq(),qd);
int d = completa(r->getDir(),qd);
/*o trecho abaixo irá retornar sempre o nó mais distante*/
/*se esquerda e direita estejam no mesmo nível ou esquerda esteja 1 nível baixo da direita retorna "e"*/
if (e==d || (e+1)==d){ return e;}
else{
/*caso a direita esteja 1 nível baixo da esquerda retorna "d"
if ((e-1)==d){ return d; }
/*caso a diferença entre os nós seja maior que 1 irá retornar 0*/
else {return 0;
}
}
}
}

int btree:: cheia(){
cheia (raiz, 0);
}
/*método muito parecido com o anterior, também se retornar ao main zero é porque a arvore está vazia ou não é cheia*/
int btree:: cheia (ptrno r, int qd){
if (r==NULL){ return qd;}/*quando chegar ao ultimo nó ou a arvore estiver vazia retorna qd*/
else{
qd++;
int e = cheia(r->getEsq(),qd);
int d = cheia(r->getDir(),qd);
/*caso os nós estejam no mesmo nível retorne "e"*/
if (e==d ){ return e;}
/*caso contrário retorna zero*/
else{return 0; }
}
}

//main

//DEGENERADA
cout << "\n" <<"Teste para ARVORE DEGENERADA:" << endl;
if (a1.Degenerada()== true)
/* Se for true imprime degenerada*/
cout << "\n" << "E' Degenerada" << endl;
else
/*se não imprime não é degenerada*/
cout << "\n" << "Nao e' Degenerada" << endl;

//CHEIA
cout << "\n" <<"Teste para ARVORE CHEIA:" << endl;
if ((a1.cheia())== 0)//se for zero a arvore ñ é cheia
cout << "\n" << "Nao e' cheia" << endl;
else
cout << "\n" << "E' cheia" << endl;

//COMPLETA
cout << "\n" <<"Teste para ARVORE COMPLETA:" << endl;
if ((a1.completa())== 0)//se for zero a arvore ñ é completa
cout << "\n" << "Nao e' completa" << endl;
else
cout << "\n" << "E' completa" << endl;

Classe main para teste dos novos métodos

/*Esse main foi feito de acordo com os valores passados no quadro na última aula no laboratório, facilitando a conferencia dos resultados impressos na tela, apos rodar o programa*/



#include
#include"btree.h"
#include
#include
#include


using namespace std;

int main()
{
btree a1; // criando o objeto a1 da classe btree

// as linhas seguintes estao inserindo valores no objeto b1 usando o metodo push

a1.push(50);
a1.push(30);
a1.push(20);
a1.push(40);
a1.push(35);
a1.push(45);
a1.push(70);
a1.push(60);
a1.push(55);
a1.push(90);



// a seguir serao impressos na tela os valores armazenados no objeto a1
// usando as tres modalidades de caminhamento.

cout << "Caminhamento Central: ESQ - RAIZ - DIR" << endl;
a1.showCentral(); cout << endl;
cout << "Caminhamento PreOrdem: RAIZ - ESQ - DIR" << endl;
a1.showPreOrdem(); cout << endl;
cout << "Caminhamento PosOrdem: ESQ - DIR - RAIZ" << endl;
a1.showPosOrdem(); cout << endl;

cout << "Imprime Folhas da Arvore" << endl;
a1.showFolhas(); cout << endl;

cout << "Programa executado!" << endl;

cout << "Imprime Representação por Parenteses Aninhados" << endl;
a1.parenteses(); cout << endl;

cout << "Imprime Representação Hierarquica II" << endl;
a1.hierarquica(); cout << endl;

cout << "Imprime Representação Hierarquica I" << endl;
a1.hiera(); cout << endl;
getch();

return 0;
}

Classe btree com novos métodos

/* Essa classe deu muito trabalho, pois dava um erro mais estranho que o outro, mas graças a ajuda do Enari, finalmente funcionou, com os ultimos metodos pedidos em sala. A representação da arvore no método parenteses foi feita de maneira recursiva, baseando-se no metodo ShowPreOrdem, apenas alterando algumas coisas como a abrtura de parenteses no inicio da chamada recursiva e fechando no retorno da chamada. A Hierarquica II (metodo hierarquica), tivemos um pouco mais de trabalho, pois não estavamos conseguindo alinhar de forma correta os caracteres na tela, mas com ajudar do Igor, ficou certinho. O Hierarquica I(metodo hiera) foi nossa "vingança" com o Igor, pois conseguimos mostrar para ele um forma mais pratica desta representação, onde fizemos nos basenado no metodo ShowCentral, apenas alternado a forma de impressão na tela.*/

#ifndef _BTREE_H
#define _BTREE_H

#include

using namespace std;

class node; // prototipo da classe node

typedef node *ptrno; // criando um tipo de dados ptrno ponteiro para node

/*
Construcao da classe node.
*/

class node{
private:
int valor;
ptrno esq, dir;
public:
node(){valor=0; esq=dir=NULL;}
node(int v){valor=v; esq=dir=NULL;}
void setValor(int v){valor=v;}
void setEsq(ptrno e){esq=e;}
void setDir(ptrno d){dir=d;}
int getValor(){return valor;}
ptrno getEsq(){return esq;}
ptrno getDir(){return dir;}
};

class btree{
private:
ptrno raiz;
// as chamadas recursivas sao privadas e soh podem ser executadas a partir de metodos do objeto.
void push(ptrno &, int);
void showCentral(ptrno);
void showPreOrdem(ptrno);
void showPosOrdem(ptrno);
void showFolhas(ptrno);
void parenteses(ptrno);
void hierarquica(ptrno, int);
void hiera(ptrno, int);
public:
btree(){raiz = NULL;}
ptrno getRaiz(){return raiz;}
// a seguir, as interfaces de funcoes recursivas
void push(int v);
void showCentral();
void showPreOrdem();
void showPosOrdem();
void showFolhas();
void parenteses();
void hierarquica();
void hiera();
};

// interface publica da funcao recursiva push (insere um novo nó na btree)
void btree::push(int v){
push(raiz, v);
}

// rotina push a ser chamada pela interface publica (insere um novo no na subarvore cuja raiz eh r
void btree::push(ptrno &r, int v){
ptrno aux;
if (r!=NULL){ // se o no atual nao for NULL, a insercao deve ser feita em uma das subarvores (esq ou dir)
if (v > r->getValor()){ // v eh maior que o valor do no e deve ser inserido na subarvore direita
aux=r->getDir();
push(aux, v);
r->setDir(aux);
}
else{ // v nao eh maior que o valor do no e deve ser inserido na subarvore esquerda
aux=r->getEsq();
push(aux, v);
r->setEsq(aux);
} // note que o objeto aux eh utilizado para recuperar possiveis alteracoes na subarvore
}
else{ // o trecho seguinte eh executado se no caminhamento pela arvore cairmos em um node NULL (r==NULL),
// o que indica que eh a posicao onde o valor deve ser inserido
aux=new(node); // usando construtor da classe node, valor=0, esq=dir=NULL (vide node())
aux->setValor(v);
r=aux;
}
}

void btree::showCentral(){
showCentral(raiz);
}

void btree::showCentral(ptrno r){ // caminhamento ESQ - RAIZ - DIR
if(r!=NULL){
showCentral(r->getEsq()); // imprime toda a subarvore ESQ com caminhamento central
cout <<>getValor() << " "; // imprime o valor armazenado na raiz
showCentral(r->getDir()); // imprime toda a subarvore DIR com caminhamento central
}
}

void btree::showPreOrdem(){
showPreOrdem(raiz);
}

void btree::showPreOrdem(ptrno r){ // caminhamento RAIZ - ESQ - DIR
if(r!=NULL){
cout <<>getValor() << " ";
showPreOrdem(r->getEsq());
showPreOrdem(r->getDir());
}
}

void btree::showPosOrdem(){
showPosOrdem(raiz);
}

void btree::showPosOrdem(ptrno r){ // caminhamento ESQ - DIR - RAIZ
if(r!=NULL){
showPosOrdem(r->getEsq());
showPosOrdem(r->getDir());
cout <<>getValor() << " ";
}
}

void btree::showFolhas(){
showFolhas(raiz);
}

void btree::showFolhas(ptrno r){ // imprime folhas por caminhamento ESQ - RAIZ - DIR
if(r!=NULL){
showFolhas(r->getEsq()); // imprime toda as folhas da subarvore ESQ com caminhamento central
if(r->getEsq()==NULL && r->getDir()==NULL) cout <<>getValor() << " "; // imprime o valor armazenado na raiz, se ela for folha
showFolhas(r->getDir()); // imprime toda as folhas da subarvore DIR com caminhamento central
}
}


//teste


void btree::parenteses(){
parenteses(raiz);
}

void btree::parenteses(ptrno r){
if(r!=NULL){
cout<< "("<<" ";

cout<getValor();

parenteses(r->getEsq());

parenteses(r->getDir());

cout<< ")"<<" ";

}

}


void btree::hierarquica(){
hierarquica(raiz, 0);
}

void btree::hierarquica(ptrno r, int x){
if(r!=NULL){

cout<
for(int i = 0; i < x*3; i++){

cout << " "; }

cout<<"|-";

cout<getValor()<
hierarquica(r->getEsq(), x+1);

hierarquica(r->getDir(), x+1);

}
}


void btree::hiera(){
hiera(raiz, 20);
}

void btree::hiera(ptrno r, int x){
if(r!=NULL){

hiera(r->getEsq(), x-3);
cout<
for(int i = 0; i < x; i++){

cout << " "; }

cout <<>getValor()<< " ";

hiera(r->getDir(), x-3);
}
}

#endif

Classe Nó

/*Segue um exemplo de classe nó */

// este eh somente um prototipo para classe no

class no;

// usado no typedef a seguir.

typedef no *ptrno; // definindo um tipo ponteiro para no

/* classe no */

class no{

//atributos da classe no

private:

int valor;

ptrno esq, dir;

public:

/* inicializa o noh com valor NULL (nulo) para nao pegar lico de memoria */

no() {valor=0; esq=NULL; dir=NULL;}

no(int i) {valor=i; esq=NULL; dir=NULL;}

//metodos para inserção de dados no nó

void setValor(int i) {valor=i;}

void setEsq(ptrno e) {esq=e;}

void setDir(ptrno d) {dir=d;}

//metodos para leitura de dados no nó

int getValor() {return valor;}

ptrno getEsq() {return esq;}

ptrno getDir() {return dir;}

};

Arvore

Arvores são estruturas de dados organizados de forma hierarquia, ele é composta de dados chamados nó. A imagem mostra um exemplo de de arvore

O nó A é chamado raiz por ser o início da arvore, os nos B, C, E, F são chamados de galhos e os nos D, G, H, I são chamados folhas por serem terminações de cada ramificação.

Numa arvore binária os nos se dividem em ate duas ramificações, a imagem acima é uma exemplo de arvore binária. O nó é constituído basicamente de 3 partes: o valor que o nó ira guardar e 2 ponteiros uma para o nó da esquerda e o outro para o nó da direita.

Exercício proposto

\*Tentei desenvolver alguns metodos, não testei nenhum, se alguem puder dra uma força, agradeço...*/

Mostre_pre(raiz)
{
if(raiz=!NULL)
{
cout<getValor();
Mostre_pre(raiz-getEsq());
Mostre_pre(raiz-getDir());
}
}

Mostre_pos(raiz)
{
if(raiz=!NULL)
{
Mostre_pre(raiz-getEsq());
Mostre_pre(raiz-getDir());
cout<getValor();
}
}

Mostre_centro(raiz)
{
if(raiz=!NULL)
{
Mostre_pre(raiz-getEsq());
cout<getValor();
Mostre_pre(raiz-getDir());
}
}
//1
Max(raiz)
{
if(raiz!=NULL)
{
int max = raiz->getValor();
Max(raiz->getDir());
}
return max;
}

//2
Min(raiz)
{
if(raiz!=NULL)
{
int min = raiz->getValor();
Max(raiz->getEsq());
}
return min;
}

//3
Quant(raiz)
{
int cont=1;
if(raiz=!NULL)
{
Quant(raiz->getEsq());
Quant(raiz->getDir());
}
cont++;
return cont;
}


//4
Altura(raiz)
{
int cont=0;
if(raiz!=NUll)
Quant(raiz->getEsq());
else
Quant(raiz->getDir());

cont++;
return cont;
}

Class Btree

// Abordagem apresentada em sala de aula

class btree {
private:
ptrno raiz;
public:
btree() { raiz=NULL;}
void push(int);
}
void btree::push(int v){
push(raiz, v);
}
void btree::(ptrno & v, int v)
{
node aux;
if(v==NULL){
v=new (node);
v->setValor(v);
v->setEsq(NULL);
v->setDir(NULL);
}

else if((v->getValor()){
aux=v->getDir();
push(aux,v);
v->setDir(aux);
}

else{
aux=v->getEsq();
push(aux,v);
v->setEsq(aux);
}
}